Question

Two airplanes leave the airport at the same time. Thirty minutes later, they are 250 miles apart. If one plane traveled 230 miles and the other plane traveled 315 miles during that time, find the angle θ between their flight paths. Show all work clearly and neatly. Round to the nearest tenth.

Answer 1

To answer this question, we can use the Cosine Law. We have that the general formula for it is as follows:

`c^2=a^2+b^2-2ab\cos C`

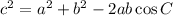
We need to remember that angle C is the angle in front of the side c. Then we have - from the graph:

• c = 250mi

,

• a = 230mi

,

• b = 315mi

And we will find the angle Θ as follows - without using units:

`250^2=230^2+315^2-2(230)(315)\cos \theta`

Then, if we solve the equation for cosΘ, we will have:

`62500=52900+99225-144900\cos \theta`
`62500=152125-144900\cos \theta`

Then, we have:

`62500-152125=-144900\cos \theta`
`-(89625)/(-144900)=\cos \theta\Rightarrow\cos \theta=0.618530020704`

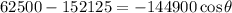
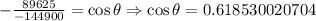
If we need to find the angle, Θ, we need to apply the inverse function of cosine, arccosine, to both sides of the equation to find it. Then, we have:

`\arccos (\cos \theta)=\arccos (0.618530020704)`

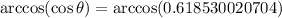
Then

`\theta=51.7911319179^(\circ)`

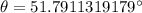
If we round the value to the nearest tenth, then we have that:

`\theta=51.8^(\circ)`

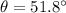
In summary, therefore, the angle Θ between their flights paths is Θ = 51.8º - rounded to the nearest tenth.