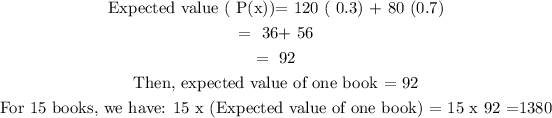SOLUTION:
Step 1:
For Part B,
Suppose that 30% of all students who have to buy a text for a particular course want a new copy (the successes!), whereas the other 70% want a used copy. Consider randomly selecting 15 purchasers.
b) What is the probability that the number who want new copies is more than two standard deviations away from the mean value?
Rounding your answer to 3 decimal places
The details of the solution are as follows:
The probability that the number who want new copies is more than two standard deviations away from the mean value means:
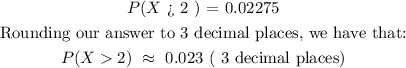
Step 3:
For Part D:
d) Suppose that new copies cost $120 and used copies cost $80.
Assume the bookstore currently has 50 new copies and 50 used copies.
What is the expected value of total revenue from the sale of the next 15 copies purchased?
[Hint: Let h(X) = the revenue when X of the 15 purchasers want new copies. Express this as a linear function.]
Indicate what rule of expected value you are using.
The correct linear function is:

The expected value of total revenue from the sale of the next 15 copies purchased =