Question

Homework:Chapter 08.4Question 5, 8.4.C-3HW Score: 18%, 4.5 of 25 pointsPoints: 0.5 of 1Question content area topPart 1Find the area of the shaded portion of the figure

Answer 1

In the given figure the diameter of the larger circle is 2.5 inches

and the diameter of the smaller circle is 0.8 inches.

The radius is given as, r = d/2 where d is the diameter.

Then,

the radius of the larger circle = R = 2.5/2 inches = 1.25 inches

and the radius of the smaller circle is = r = 0.8/2 inches = 0.4 inches

Now the area of the circle is given as

`\begin{gathered} A=\pi r^2 \\ where\text{ r is the radius of the circle} \end{gathered}`

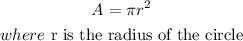
So the area of the shaded portion will be

`\begin{gathered} Required\text{ area=}\pi R^2-\pi r^2 \\ Required\text{ area = }\pi[R^2-r^2]=(22)/(7)*[1.25^2-0.4^2] \\ Required\text{ area =3.14}*1.4025\text{ sq inches} \\ Required\text{ area = 4.40385 sq inches} \end{gathered}`

Hence the area of the shaded portion will be 4.40385 sq inches.