Answer:
601.379 m²/min
Step-by-step explanation:
The area of the circle is calculated as

Where r is the radius. To find the rate of change, we need to derivate the expression, so
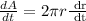
Now, we need to find r when the area is 81π², so solving the following equation for r, we get:
![\begin{gathered} 81\pi^2=\pi r^2 \\ (81\pi^2)/(\pi)=(\pi r^2)/(\pi) \\ 81\pi=r^2 \\ \sqrt[]{81\pi}=r \\ 9\sqrt[]{\pi}=r \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/nlr03endpidprk9fg5duq6t8ajb3cvuyql.png)
Then, we can find dA/dt when the area is 81π², replacing r = 9√π and dr/dt by 6 m/min
![\begin{gathered} \frac{\text{ dA}}{\text{ dt}}=2\pi(9\sqrt[]{\pi})(6) \\ \frac{\text{ dA}}{\text{ dt}}=601.379^{}m^2\text{/min} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/41tfvca39he3njhmhk5inumq96200i07kl.png)
Therefore, the rate of change is 601.379 m²/min