Given the system of equations as shown below
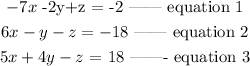
The above system of equations can be expressed in the matrix form
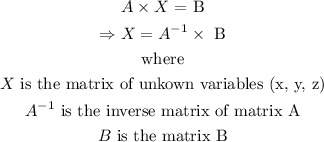
Thus, we have
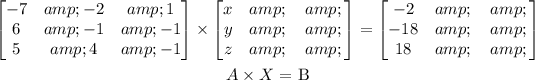
This implies that
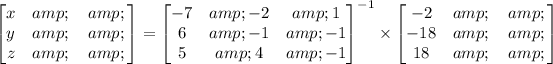
Where
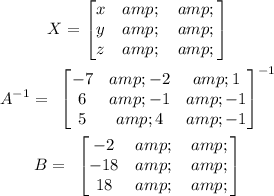
Solving for X Using crammer's rule, which states that
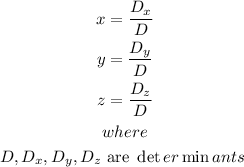
To find the deteminant D,
From the matrix A,
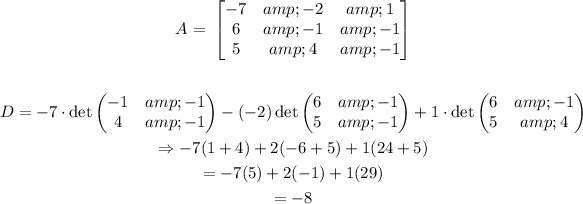
Thus, D = -8
To find x,
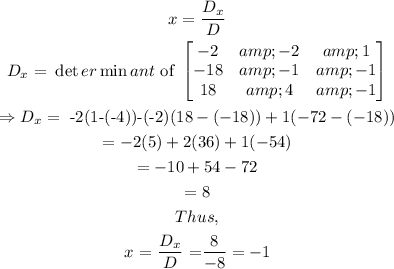
To find y,
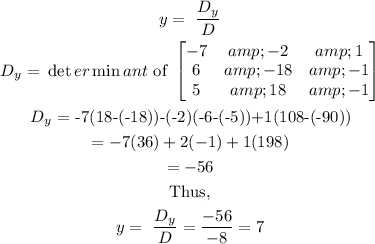
To find z,
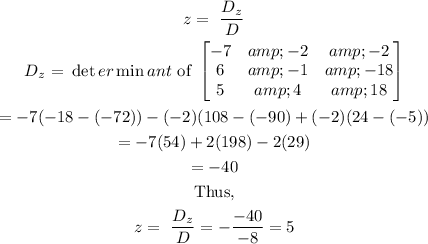
Hence, the solution to the system of equations is
(-1, 7, 5).
The correct option is B.