Question

complete the statement given the information below . The given angles options are 1. corresponding angels 2. Alternate interior angles 3. same side interior angles and x options are 1. 7° 2. 18° 3.43°

Answer 1

The lines "a" and "b" shown in the picture are parallel and crossed by a transversal line.

The angle that measures 65º and the adjacent angle to the one that measures (x+72)º are corresponding angles, which means that they are congruent.

Both adjacent angles are supplementary, which means that they add up to 180º

`65º+(x+72)º=180º`

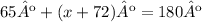
From this expression, you can determine the value of x, first, take the parentheses away and add the like terms:

`\begin{gathered} x+65+72=180 \\ x+137=180 \end{gathered}`

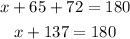
Next, subtract 137 from both sides of the equation:

`\begin{gathered} x=180-137 \\ x=43 \end{gathered}`

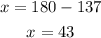
The value of x is 43 and the measure of the given angle is:

x+72 = 43+72 = 115º