Step-by-step explanation:
The quadratic equation is of the form,
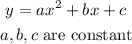
a) For the first option, The given data represents the relation,
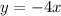
So, it is not the quadratic equation.
b) From the table, the relation is,
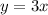
Not a quadratic equation.
c) to find the quadratic equation,
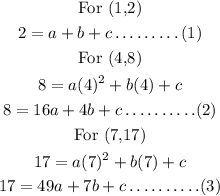
Solving these questions,
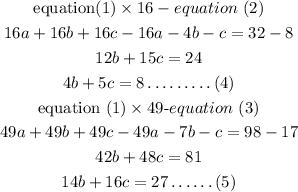
Now solve equation (4) and (5),
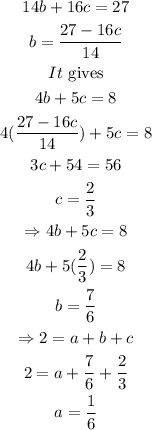
So, the equation is,
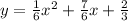
d) The data represents the relation,
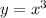
Not a quadratic equation.
Answer: option c)