Question

Question 6 (1 point)Using the Triangular Prism in the picture, find the Lateral Area, the Area of a Single Base, and the TOTAL Surface Area:12 in5 in-4 in?? inFirst find the missing length=____________inLateral Area =in²Single Base Area =_in²Surface Area =Blank 1:in²

Answer 1

Explanation

We are given the following:

`\begin{gathered} Lateral\text{ }triangle:\begin{cases}{height=12\text{ }in} \\ {base=5\text{ }in} \\ {hypotenuse=?}\end{cases} \\ \\ Left\text{ }lateral\text{ }rectangle:\begin{cases}length={12\text{ }in} \\ width={4\text{ }in}\end{cases} \\ \\ Right\text{ }lateral\text{ }rectangle:\begin{cases}length={5\text{ }in} \\ width={4\text{ }in}\end{cases} \\ \\ Base\text{ }rectangle:\begin{cases}length={?} \\ width={4\text{ }in}\end{cases} \end{gathered}`

We are required to determine the following:

• The missing length of the triangle.

,

• The lateral area.

,

• The single base area.

,

• The surface area of the figure.

We know that we can determine the missing length of the triangle by using the Pythagorean theorem as follows:

`\begin{gathered} Hyp.^2=Opp.^2+Adj.^2 \\ hyp.^2=height^2+base^2 \\ hyp.^2=12^2+5^2 \\ hyp.^2=144+25 \\ hyp.^2=169 \\ hyp.=√(169)=13\text{ }in \\ Note:\text{ }the\text{ }hypotenuse\text{ }of\text{ }the\text{ }triangle=length\text{ }of\text{ }rectangular\text{ }base \end{gathered}`

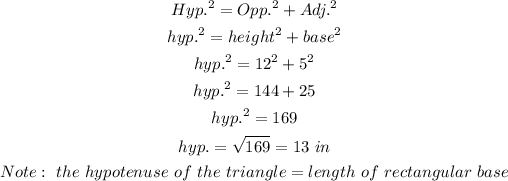
Hence, the missing length of the triangle (hypotenuse) is 13 in.

Next, we determine the lateral area as follows:

`\begin{gathered} Area=Area\text{ }of\text{ }lateral\text{ }triangles+Area\text{ }of\text{ }lateral\text{ }rectangles \\ Area=2((1)/(2)bh)+(lw)+(lw) \\ Area=2((1)/(2)*5*12)+(12*4)+(5*4) \\ Area=2(30)+48+20 \\ Area=60+48+20=128\text{ }in^2 \end{gathered}`

Hence, the lateral area is 128 in².

The area of the single base can be calculated as:

`\begin{gathered} Area=lw \\ Area=13*4 \\ Area=52\text{ }in^2 \end{gathered}`

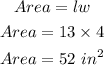
Hence, the single base area is 52 in².

Finally, the surface area of the figure is:

`\begin{gathered} Surface\text{ }Area=Area\text{ }of\text{ }lateral\text{ }faces+Area\text{ }of\text{ }base \\ Surface\text{ }Area=128+52 \\ Surface\text{ }Area=180\text{ }in^2 \end{gathered}`

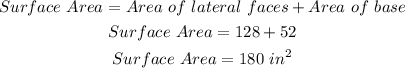
Hence, the surface area is 180 in².