It is required to construct a probability distribution for a discrete random variable of a family that has three children.
Let the random variable X represent the number of boys.
The sample space is given as:
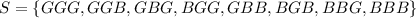
Since X represents the number of boys, the probability P(X) for X=0, is the probability that the family has 0 boys, that is, GGG:
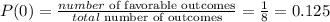
Follow the same procedures for one, two, and three boys to construct the table below:

Notice that the sum of P(X)=1. This must be so since it is a probability distribution.
The probability of getting at least one boy is:
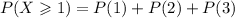
Substitute the probabilities:
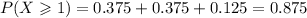
The required probability is 0.875