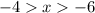1.

we separate the inequality into two parts to solve the absolute value
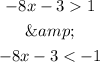
first part

second part
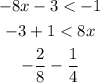
graph
where the yellow lines are the first part, red the second part and the solution of the inequality is the union of these two
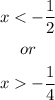
2.
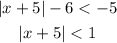
we separate the inequality into two parts to solve the absolute value
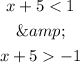
first part
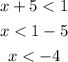
second part
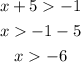
graph
where the first part is yellow, the second part is red and the solution of the inequality is green