Two triangles are similar when the corresponding angles are congruents and the corresponding sides are in proportion:
Then, you have the next corresponding sides:
JK and KL
TJ and LM
TK adn KM
To find the value of x that makes the corresponding sides TJ and LM be proportional, you use the next formula that shows the proportionaliti between the triangles TJK and KLM:
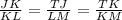
As you know the measure of the sides JK and KL, you use that values, as follow:
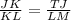
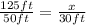
Then, you clear the x:
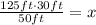
And calculate the value of x:
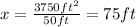
Then, the value of x that proves the triangles above are similar is x=75ft