The general equation of a line with slope m and y-intercept b is:

Where the slope m of a line that passes thorugh two points (x_1,y_1) and (x_2,y_2) is given by:

Use the coordinates of the points (0,6) and (1,8) to find the slope of the desired line:
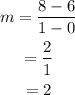
The y-intercept is the value at which the line crosses the y-axis when x=0. Since the point (0,6) is already being considered, we know that b=6.
Substitute m=2 and b=6 into the equation of a line in slope-intercept form:
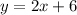
Therefore, y=2x+8 is the equation of a line containing (0,6) and (1,8).