Question

P. A 300 kg pig is standing at the top of a muddy hill on a rainy day. The hill is 80 meters long

with a vertical drop of 20 meters. The pig begins to slide in the mud down the hill. Ignoring
friction, how fast will our poor pig be moving when it reaches the bottom of the hill?

Answer 1

Given data:

* The height of the hill is h_i = 20 meters.

* The length of the hill is L = 80 meters.

* The mass of the pig is m = 300 kg.

* The initial velocity of the pig is u = 0 m/s.

* The final height of the pig is h_f = 0 meters.

Solution:

The net energy of the system at the top of the hill is,

`E_i=mgh_i+(1)/(2)mu^2`

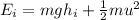
where g is the acceleration due to gravity,

Substituting the known values,

`\begin{gathered} E_i=300*9.8*20+0 \\ E_i=58800\text{ J} \end{gathered}`

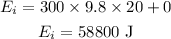
The net energy of the system at the bottom of the hill is,

`E_f=\text{mgh}_f+(1)/(2)mv^2`

where v is the final velocity of the pig,

Substituting the known values,

`\begin{gathered} E_f=0+(1)/(2)*300* v^2 \\ E_f=150v^2 \end{gathered}`

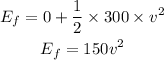
According to the law of conservation of energy,