Question

Given that -9 I as a zero, factor the following polynomial function completely

Answer 1

Given: -9i zero and

`f(x)=x^4+11x^3+99x^2+891x+1458`

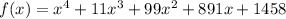
Find: root of the given eqaution.

Step-by-step explanation: if -9i is thr one root of the equation then 9i wll be the another root of the equation.

-9i (x+9i)

9i (x-9i)

that means (x+9i)(x-9i) will be divide by the given equation.

`(x+9i)(x-9i)=(x^2+81)`

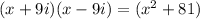
when we divide it to the given equation we get,

`x^2+11x+18`

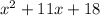
on solving it

`\begin{gathered} x^4+11x^3+99x^2+891x+1458=(x+9i)(x-9i)(x^2+11x+18) \\ =(x+9i)(x-9i)(x+2)(x+9) \end{gathered}`

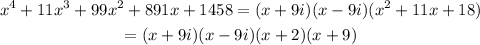
Hence,the other roots of the given eqaution is -2 and -9.

Final answer: the required roots of the equation is 9i,-9i,-2,-9.