Question

Solve the polynomial equation give all solutions real and imaginary x^3+64=0

Answer 1

`\begin{gathered} x=-4 \\ x=2+2\sqrt[]{3i} \\ x=2-2\sqrt[]{3i} \end{gathered}`

Step-by-step explanation

We want to solve the polynomial:

`x^3+64=0`

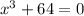
First, subtract 64 from both sides of the equation:

`\begin{gathered} x^3+64-64=0-64 \\ x^3=-64 \end{gathered}`

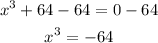
For a cubic polynomial in the form x³ = f(a), the solutions are:

`x=\sqrt[3]{f\left(a\right)},\: \sqrt[3]{f\left(a\right)}(-1-√(3)i)/(2),\: \sqrt[3]{f\left(a\right)}(-1+√(3)i)/(2)`

From the given polynomial, f(a) = -64

Therefore, the solutions of the polynomial are:

`\begin{gathered} x=\sqrt[3]{-64};,\: \sqrt[3]{-64}\frac{-1-\sqrt[]{3}i}{2};\text{ }\sqrt[3]{-64}\frac{-1+\sqrt[]{3}i}{2} \\ \Rightarrow x=-4;-4\cdot\frac{-1-\sqrt[]{3}i}{2};-4\cdot\frac{-1+\sqrt[]{3}i}{2} \\ \Rightarrow x=-4;-2\cdot-1-\sqrt[]{3}i;-2\cdot-1+\sqrt[]{3}i \\ \Rightarrow x=-4;x=2+2\sqrt[]{3i};x=2-2\sqrt[]{3i} \end{gathered}`

Those are the solutions.