Question

A scientist want to know if there is a magningful difference between two groups of gels that grow bacteria. He randomly selects six gels from each group, and counts the number of bacteria spots on each gel; Group A: 9,12,13,13,14,17Group B: 8,6,5,8,13,8Is there a magningful difference between the two groups? Show all calculation that lead to your answer.

Answer 1

We will be calculating an Independent Samples t-test to determine whether or not there is a meaningful (or significant) difference between the two groups

Step 1: Sum the two groups (separately)

Group A: 9 + 12 + 13 + 13 + 14 + 17 = 78

Group B: 8 + 6 + 5 + 8 + 13 + 8 = 48

Step 2: Square the sums from Step 1

(78)^2 = 6084

(48)^2 = 2304

Set these numbers aside for a moment.

Step 3: Calculate the means for the two groups

Group A: (9 + 12 + 13 + 13 + 14 + 17)/6 = 78/6 = 13

Group B: (8 + 6 + 5 + 8 + 13 + 8)/6 = 48/6 = 8

Set these numbers aside for a moment.

Step 4: Square the individual scores and then add them up

Group A: 9^2 + 12^2 + 13^2 + 13^2 + 14^2 + 17^2 = 1048

Group B: 8^2 + 6^2 + 5^2 + 8^2 + 13^2 + 8^2 = 422

Set these numbers aside for a moment.

Step 5: Insert your numbers into the formula below and solve

`t\text{ = }\frac{\mu_A-\mu_B}{\sqrt[]{(\frac{(\sum^{}_{}A^2-\frac{(\sum^{}_{}A)^2}{N_A})\text{ + }(\sum^{}_{}B^2-\frac{(\sum^{}_{}B)^2}{N_B})\text{ }}{\N_{A\text{ }}+N_B\text{ - }2})\text{ }*((1)/(N_A)+(1)/(N_B))}}`

(ΣA)^2: Sum of data set A, squared (Step 2).

(ΣB)^2: Sum of data set B, squared (Step 2).

μA: Mean of data set A (Step 3)

μB: Mean of data set B (Step 3)

ΣA^2: Sum of the squares of data set A (Step 4)

ΣB^2: Sum of the squares of data set B (Step 4)

NA: Number of items in data set A

NB: Number of items in data set B

`t\text{ = }\frac{13_{}-8}{\sqrt[]{(\frac{(1048^{}-\frac{(78)^2}{6_{}})\text{ + }(422^{}-\frac{(48)^2}{6_{}})\text{ }}{6\text{ }_{}+6\text{ - }2})\text{ }*(\frac{1}{6_{}}+\frac{1}{6_{}})}}`
`t\text{ = }\frac{5}{\sqrt[]{(\frac{(34_{})\text{ + }(38)\text{ }}{10})\text{ }*(\frac{2}{6_{}}_{})}}`
`t\text{ = }\frac{5}{\sqrt[]{2.4}}`

`t\text{ = 3.227}`

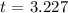
Step 6: Find the Degrees of freedom

NA-1 + NB-1) = (6-1 + 6 - 1) = 10

Step 7: Look up your degrees of freedom (obtained in Step 6) from the t-table. Since we don’t know what the alpha level is, we will use 5% (0.05).

From the t-table, 10 degrees of freedom at an alpha level of 0.05 = 2.23

Step 8: Compare the calculated value ( from Step 5) to the table value (Step 7).

The calculated t value of 3.227 is more than the cutoff of 2.23 from the table. Therefore p <0.05.

As the p-value is less than the alpha level, we can conclude that there is a statistically significant difference between the two groups