minimum:10
output :509
maximum:5
output: 634
Step-by-step explanation
Step 1
graph the function:
to do this, you need put values for x, and you will get a set of values for y, those formed pairs are the coordinates,
we can see, there are a minimun and a maximum
Step 2
find the minimum
To find the local minimum of any graph, you must first take the derivative of the graph equation, set it equal to zero and solve for
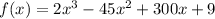
a) derivate
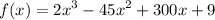
To take the derivative of this equation, we must use the power rule
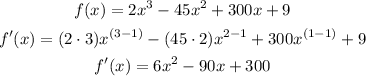
solve for x by applying the quadratic formula
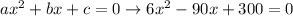
![\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ \text{replace} \\ x=\frac{-(-90)\pm\sqrt[]{90^2-4\cdot6\cdot300}}{2\cdot6} \\ x=\frac{90\pm\sqrt[]{8100-7200}}{12} \\ x=\frac{90\pm\sqrt[]{900}}{12} \\ x=(90\pm30)/(12) \\ so \\ x_1=(90+30)/(12)=(120)/(12)=10 \\ x_2=(90-30)/(12)=(60)/(12)=5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/t292cy8zh8tv1uowjcqfnmyeppookd6mwe.png)
then, let's find the output when x=5
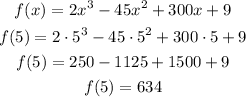
so,infelection point is (5,634)
Step 3
Now, the output when x=10
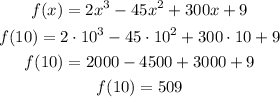
inflection point (10,509)
Step 3
so, at x=5 and x=10 we have two inflection points, to know if those points are minimum we need to check the second derivate of the fucntion
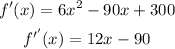
now, check if f''(x) is greater than zero
a)at x=5
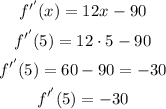
it is smaller than zero, it means (5,634) is a maximum
b)at x=10
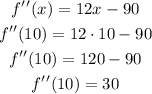
it is greater than zero, it means (10,509) is a minimum
I hope this helps you