First, we need to convert 253 lb to kilograms. Given that 1 kg is equivalent to 2.205 lb, then:
![253\text{ lb = }253\text{ lb}\cdot\frac{1\text{ kg}}{2.205\text{ lb}}\approx114.74\operatorname{kg}]()
The dosage Justin should receive is directly proportional to his weight. Given that a dosage of 11 mg corresponds to a weight of 20 kg, then to find the dosage that corresponds to 114.74 kg we can use the next proportion:
![\frac{11\text{ mg}}{x\text{ mg}}=\frac{20\operatorname{kg}}{114.74\operatorname{kg}}]()
Solving for x:
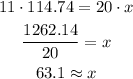
He should receive a dosage of 63.1 mg