Question

A club needs to choose 3 members to be president, vice president and treasurer. If there are 15people in the club, how many ways can they assign the three rolls?

Answer 1

Given:

Total people in the club = 15

Number of choices = 3

Let's find the number of ways they can assign the three rolls.

To find the number of ways, apply the permutation formula since there can be replacement in this situation.

`^nP_r=(n!)/((n-r)!)`

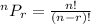
Where:

n = 15

r = 3

Thus, we have:

`\begin{gathered} ^(15)P_3=(15!)/((15-3)!) \\ \\ =(15!)/(12!) \\ \\ =(15*14*13*12!)/(12!) \\ \\ =15*14*13 \\ \\ =2730 \end{gathered}`

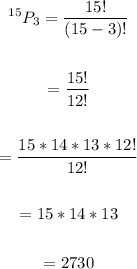
Therefore, there are 2730 ways they can assign the three roles.

ANSWER:

b. 2730