the length of the rectangular base is 2.5 times of width
let the width is b = x
then length is l = 2.5x
the volume of the box is 650 cm^2
let the height is h
so volume is
l x b x h = 650
(2.5x) (x) h = 650
h = 650/2.5x^2650
now the area of the base is
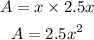
the cost of the base is 6 cents/ cm^2
now the total cost is,
6 (2.5x^2) = 15x^2
area of the sides is
A= 4 (l x h)
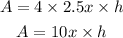
cost of the side is 6 cents/ cm^2
so total cost os sides are (10x)h
so total cost of the box is
15x^2 + 10xh
now, put the value of h
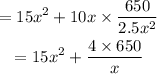
for minimizing the cost
differentiate the above expression
30x - 2600/x^2 =0
from here x = 4.42
now the dimension are
b= 4.42
l = 2.5 x 4.42 = 11.05
h = 13.30