Equation of the line
The equation of a line in slope-intercept form is:
y = mx + b
Where m is the slope and b is the y-intercept.
We are required to find the equation of a line that is perpendicular to the line
y = 5x + 4
and passes through the point (-5,2)
The first thing we need to do is to calculate the slope of the required line.
The slope of the given line is m1=5. Two lines are perpendicular if their slopes satisfy the equation:
m1 * m2 = -1
Solving for m2:

The equation of the required line is:
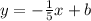
To find the value of b, we substitute the given point (-5,2):
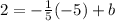
Operating:
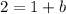
Solving for b:
b = 1
Finally, our equation is:
