The magnitude and direction of −4w are 928 and 224°, respectively.
To find the magnitude and direction of −4w, we can first find the magnitude and direction of w. The magnitude of w is given by the Pythagorean theorem:
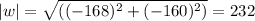
The direction of w is given by the following equation:
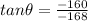 = 0.947
= 0.947
Solving for θ, we get:
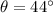
Therefore, the magnitude and direction of w are 232 and 44°, respectively.
To find the magnitude and direction of −4w, we simply multiply the magnitude of w by −4 and add 180° to the direction of w.
The magnitude of -4w is
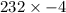 = -928.
= -928.
The direction of -4w is
 .
.