Given the word problem, we can deduce the following information:
Perimeter of the rectangle = 254 yards
L = 2W-8
where:
W=width
L=Length
To determine the dimensions, we first note that the formula for the rectangle's perimeter is:
P=2(L+W)
where:
P=Perimeter
L=Length
W=Width
So,
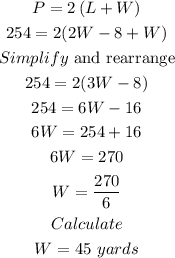
Next, we plug in w=45 into L = 2W-8:
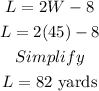
Therefore, the dimensions are:
Length=82 yards
Width = 45 yards