Question

There are 13 players on the volleyball team. Six players are actively on the court at any given time. How many different ways can 6 players be chosen from a group of 13 ?

Answer 1

The difference between combination ad permutation is that the order arrangement matters in a permutation, but in a combination, it does not. So this is a combination because we do not need to arrange the volleyball players in a specific way

So:

`\begin{gathered} nCr=\frac{n!}{r!(n\text{ -}r)!} \\ nCr=\frac{13!}{6!(13\text{ -}6)!} \\ nCr=(13(12)(11)(10)(9)(8)(7!))/(6!(7!)) \\ nCr=(13(12)(11)(10)(9)(8))/(6(5)(4)(3)(2)(1)) \\ nCr=(1235520)/(720) \\ nCr=1716 \end{gathered}`

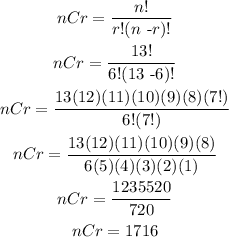
n is the number of objects

and r is the number of selected objects.

In tota, there are 1716 ways in which you can arrange 6 players from a group of 13 people.