Question

46. Coordinate Geometry The x- and y-axes of the coordinate plane form four right angles. The interior of each of the right angles is a quadrant of the coordinate plane. What is the equation for the line that contains the angle bisector of Quadrants I and III?

Answer 1

y=x

Step-by-step explanation

f(x)=?

Step 1

the angle bisector is the line or line segment that divides the angle into two equal parts, then we have half of 90 degrees

if you know the angle formed by a line with x-axis you can find the slope using:

`\begin{gathered} \text{slope}=\tan \alpha\text{ }\cdot \\ \end{gathered}`

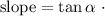
replace

`\begin{gathered} \alpha=45\~ \\ \text{slope}=\tan \text{ 45=1} \\ \text{slope =1} \end{gathered}`

now, we have the slope of the line

Step 2

Also, the line crosses the origin(0,0), then, we have a point of the line

Step 3

fin the equation using

slope=1

point of the line (0,0)

`\begin{gathered} y-y_0=m(x-x_0) \\ \text{where} \\ m\text{ is the slope } \\ (x_1,y_1)\text{ are the coordinates of the known point} \end{gathered}`

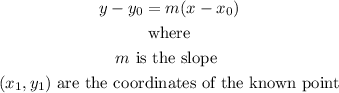
replace

`\begin{gathered} y-0=1(x-0) \\ y-0=1x-1\cdot0 \\ y=1x \\ y=x \end{gathered}`

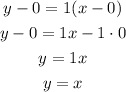
so, the equation is y=x