Given the forces:
300 N at 0 degrees
400 N at 90 degrees
Let's solve for part C and D.
Part c.
The magnitude of the resultant force.
To find the magnitude of the resultant force, apply the formula:
![F_R=\sqrt[]{F^2_x+F^2_y}](https://img.qammunity.org/2023/formulas/physics/college/b5j3361w2kcme436rpka64en0lc1o881oe.png)
Where:
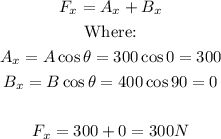
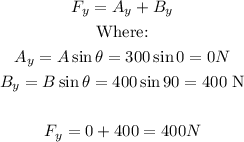
Fx = 300
Fy = 400
Hence, we have:
![\begin{gathered} F_R=\sqrt[]{(300)^2+(400)^2} \\ \\ F_R=\sqrt[]{90000+160000} \\ \\ F_R=\sqrt[]{250000} \\ \\ F_R=500\text{ N} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/eob2khemd4st5s1xzzyb39qsslepr6hg2d.png)
Therefore, the magnitude of the resultant force is 500 N.
• Part d.
The direction of the resultant force.
To find the direction of the resulatnt force, apply the fomula(trig ratio for tan):
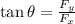
Hence, we have:
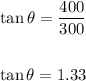
Take the tan inverse of both sides:
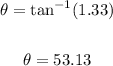
Therefore, the direction of the resultant force is 53.13° from the x-axis.
ANSWER:
(c) 500 N
(d) 53.13°