The given problem can be exemplified in the following diagram:
We are given that an elevator is moving upwards and we are required to determine the acceleration. To do that we will sum all the forces in the vertical direction taking upwards as positive and downwards as negative and, according to Newton's second law of motion this sum must be equal to the product of the mass of the elevator and its acceleration, like this:
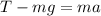
Where:
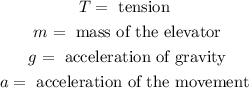
Now we solve for the tension by adding "mg" to both sides and we get:
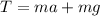
Now we take "m" as a common factor:
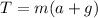
To determine the acceleration "a" we use the graph of motion. Since the graph is a linear graph of velocity vs time this means that the acceleration is the slope of the graph. To determine the slope of the graph we use the following equation:
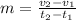
Where:
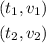
Are any two points in the graph. We choose the following points:
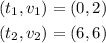
Replacing in the formula for the slope:
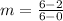
Solving the operations we get:

Therefore, the acceleration is:
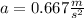
Now we replace in the expression for the tension "T":
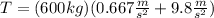
Solving the operations we get:
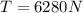
Therefore, the tension in the elevator is 6280 Newtons.