Question

For the Y coordinate the options are 7,4,0,3.I just need a brief explanation with the answer

Answer 1

we have that

JK=JP+PK -----> by the three points are collinear

and

JP/JK=1/3 -----> JK=3JP -----> equation A

substitute

3JP=JP+PK

2JP=PK ------> equation B

Find out the distance JK

we have

J(-4,11) and K(8,-1)

substitute in the formula of distance between two points

`JK=\sqrt[\square]{(-1-11)^2+(8+4)^2}`
`JK=12\sqrt[\square]{2^{}}`

equation A

JK=3JP

`\begin{gathered} 12\sqrt[\square]{2}=3JP \\ JP=4\sqrt[\square]{2} \end{gathered}`

we have the distance JP

substitute in the formula of distance

`4\sqrt[\square]{2}=\sqrt[\square]{(x+4)^2+(y-11)^2}`

squared both sides

`32=(x+4)^2+(y-11)^2\text{ ----}\longrightarrow\text{ equation C}`

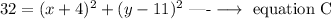
equation B

2JP=PK

`2(4\sqrt[\square]{2})=\sqrt[\square]{(x-8)^2+(y+1)^2}`

squared both sides

`128=(x-8)^2+(y+1)^2\text{ ---}\longrightarrow\text{ equation D}`

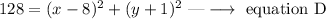
Solve the system of equations C and D

the graphs are circles

the solution is the intersection points both graphs

see the attached figure to better understand the problem

the solution is the point (0,7)

the coordinates of P are (0,7)