Question

Part IOnce you have constructed the parabola, use GeoGebra to display its equation. In the space below, rearrange the equation of the parabola shown in GeoGebra, and check whether it matches the equation in the vertex form that you wrote in part G. Show your work.How do I rearrange the equation?Here's the equation: y = 1/12 ( x - 6 )^2 +1

Answer 1

Given

`1.33x^2-16x-16y=-64`

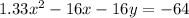
Transform it into its vertex form as shown below

`\begin{gathered} \Rightarrow16y=1.33x^2-16x+64 \\ \Rightarrow y=(1.33)/(16)x^2-x+4 \end{gathered}`

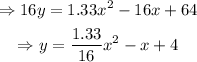
Complete the square on the right side of the equation,

`\begin{gathered} \\ \\ Set\text{ }b\text{ the term that completes the square} \\ \\ \\ \Rightarrow ax^2-2abx+ab^2=(1.33x^2)/(16)-x+c \end{gathered}`
`\begin{gathered} \Rightarrow a=(1.33)/(16) \\ -2abx=-x \\ \Rightarrow2ab=1 \\ \Rightarrow b=(1)/(2a) \\ \Rightarrow b=(16)/(2*1.33) \end{gathered}`

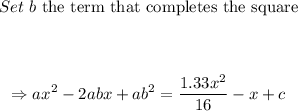
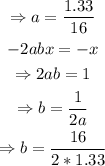
Therefore,

`\begin{gathered} \Rightarrow y=(1.33)/(16)x^2-x+4=(1.33)/(16)(x-(8)/(1.33))^2-((8)/(1.33))^2+4 \\ \Rightarrow y=(1.33)/(16)(x-(8)/(1.33))^2-(((8)/(1.33))^2-4) \end{gathered}`

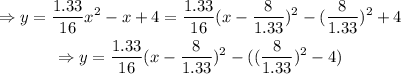
Thus, the obtained equation does not match the equation found in part G.

However, consider that the leading coefficient is 1.33=1/3

Then, the given expression becomes

`\begin{gathered} (1)/(3)x^2-16x-16y=-64 \\ \end{gathered}`

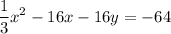
By the same token,

`\begin{gathered} \Rightarrow y=(1)/(48)x^2-x+4 \\ \end{gathered}`

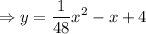
Completing the square,

`(1)/(48)(x^2-48x)+4=(1)/(48)(x-24)^2-8`