Question

In the country of United States of Heightlandia, the height measurements of ten-year-old children are approximately normally distributed with a mean of 53.9 inches, and standard deviation of 3 inches.A) What is the probability that a randomly chosen child has a height of less than 47.4 inches?Answer= (Round your answer to 3 decimal places.)B) What is the probability that a randomly chosen child has a height of more than 59.1 inches?Answer= (Round your answer to 3 decimal places.)

Answer 1

Given:

`\begin{gathered} \mu=53.9 \\ \sigma=3 \\ x=47.4 \end{gathered}`

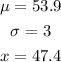
Part A:

Find the Z-score

`\begin{gathered} Z=(x-\mu)/(\sigma) \\ Z=(47.4-53.9)/(3) \\ Z=(-6.5)/(3) \\ Z=-2.1667 \end{gathered}`

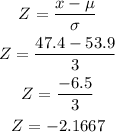
From the Z-scores table, the probability of the height less than 47.4 inches is;

Find the Z-score

`\begin{gathered} Z=(x-\mu)/(\sigma) \\ Z=(59.1-53.9)/(3) \\ Z=(5.2)/(3) \\ Z=1.7333 \end{gathered}`

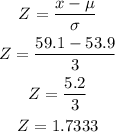
From the Z-scores table, the probability that the height of more than 59.1 inches is;

`\begin{gathered} P(x>Z)=0.041521 \\ \\ To\text{ 3 decimal places;} \\ P(x>Z)=0.042 \end{gathered}`

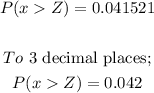
Therefore, the probability that a randomly chosen child has a height of more than 59.1 inches is 0.042