Question

a rectangular garden with an area of 48 ft has a width equal to 1/3 its length. What is the measure of the diagonal of the garden? Express your answer as a decimal to the nearest hundredth.

Answer 1

Given the area of the rectangular garden:

`A=48ft`

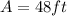
You know that its width is:

`w=(1)/(3)l`

Where "l" is the length of the rectangular garden.

Let be "d" the length (in feet) of the diagonal of the garden.

You can draw the rectangle described in the exercise:

By definition, the area of a rectangle can be calculated using this formula:

`A=lw`

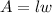
Where "l" is the length and "w" is the width.

In this case, substituting the expression that corresponds to "w" and the area of the rectangular garden into the formula, you get this equation:

`48=l((1)/(3)l)`

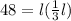
Now you can solve for "l" in order to find its value:

`\begin{gathered} 48=(1)/(3)l^2 \\ \\ (3)(48)=l^2 \\ \sqrt[]{144}=l \\ \\ l=12ft \end{gathered}`

By definitio