Question

a student incorrectly says the solution to the equation -3/4y-1/7y=700 y=625 What error did the student make?

Answer 1

Given the equation:

`-(3)/(4)y-(1)/(7)y=700`

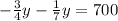
To determine the value of y, you have to simplify both like terms first, that is to subtract -1/7y from -3/4y

`-(25)/(28)y=700`

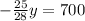
Next is to divide both sides of the equation by -25/28, which is the same as multiplying them by -28/25

`\begin{gathered} -(25)/(28)y\cdot(-(28)/(25))=700\cdot(-(28)/(25)) \\ y=-784 \end{gathered}`

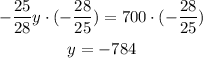
The error of the student is that he multiplied both sides of the equation by a positive fraction and did not use the reciprocal fraction. Correct option is A. He multiplied 700 by 25/28