Question

Write the rule for the nth term and the 7th term of the sequence 6 24 96 384 1536

Answer 1

Given

The sequence,

6, 24, 96, 384.

To find the nth term of the sequence.

Step-by-step explanation:

It is given that,

The sequence is,

6, 24, 96, 384.

That implies,

`(24)/(6)=(96)/(24)=(384)/(96)=4`

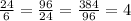
Then, the given sequence is a GP.

Therefore,

The nth term of the given sequence is,

`\begin{gathered} a_n=ar^(n-1) \\ =6(4)^(n-1) \end{gathered}`

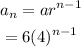
That implies,

`\begin{gathered} a_7=ar^(7-1) \\ =6(4)^6 \\ =6*4096 \\ =24576 \end{gathered}`

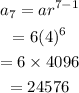
Hence, the seventh term of the sequence is 24576.