A half turn about the origin is the same thing as say a rotation about the origin of 180°. To calculate the point of each image, we can do it in two ways. Let me show it:
Say we have a counterclockwise rotation of θ. We can find the image of a point by using these equations:
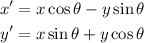
Where x and y is the original point and x' and y' is the image. For 180°, we have:
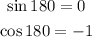
So, the equations simplify to:
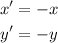
The second way is by just seeing that a 180° turn would get you to opposite quadrant, changing the signs of each coordinate. So, both methods are equivalent.
Now, for the points:
a. (0,4):
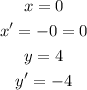
So, (0,-4).
b. (-1,3):
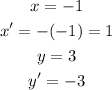
So, (1,-3)
c. (-x, -y): here, it is simply change the sign:
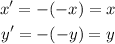
So, (x,y).