Question

Hi there, I cannot get this answer correct and I have no idea where I am going wrong.

Answer 1

Given

AB = 18 , CD = 10

diameter = 30

Find

How much closer is AB than CD to point O.

Step-by-step explanation

Radius = 15

AO = 15 , CO = 15

In right angle triangle , OFB ,

`\begin{gathered} AO^2=OP^2+FB^2 \\ 15^2=OP^2+9^2 \\ 225-81=OF^2 \\ 144=OF^2 \\ OF=12 \end{gathered}`

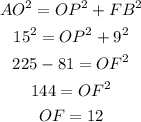
and in right triangle OED

`\begin{gathered} OD^2=OE^2+ED^2 \\ 15^2=5^2+OE^2 \\ 225-25=OE^2 \\ 200=OE^2 \\ OE=14.1421356237 \\ \end{gathered}`

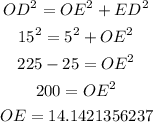
subtract the length of OF - OE = 14.1421356237 - 12 = 2.14213562373

Final Answer

Hence , the length AB is 2.14 cm closer than CD to point O