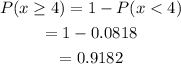Question

The number of hits to a website follows a Poisson process. Hits occur at the rate of1.4 per minute between 7:00 P.M. and 10:00 P.M. Given below are three scenarios for thenumber of hits to the website. Compute the probability of each scenario between 9:30 PM and9:35 P.M. Interpret each result.(a) exactly four(b) fewer than four(c) at least four

Answer 1

Given that:

Rate at which the hits occur between 7 PM and 10 PM = 1.4 per minute

Then:

Number of hits between 9:30 AM and 9:35 AM

`\begin{gathered} =5\cdot(1.4) \\ =7 \end{gathered}`

The probability distribution function of Poisson distribution is

`P(X=x)=(e^(-\lambda)\lambda^x)/(x!)`

(a) P(x=4)

`\begin{gathered} =(e^(-7)7^4)/(4!) \\ =0.0912 \end{gathered}`

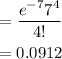
(b) P(x < 4) = P(x=0)+P(x=1)+P(x=2)+P(x=3)

`\begin{gathered} =(e^(-7)7^0)/(0!)+(e^(-7)7^1)/(1!)+(e^(-7)7^2)/(2!)+(e^(-7)7^3)/(3!) \\ =e^(-7)+7e^(-7)+(49e^(-7))/(2)+(343e^(-7))/(6) \\ =0.0818 \end{gathered}`

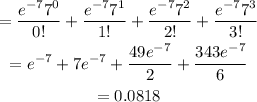
(c) To find

`\begin{gathered} P(x\ge4)=1-P(x<4) \\ =1-0.0818 \\ =0.9182 \end{gathered}`