Question

At his son's birth, a man invested $2,000 in savings at 6% for his son's college education.

Approximately how much, to the nearest dollar, will be available in 19 years? Rounded to the nearest year, approximately how long will it take for the man’s investment to double?

Answer 1

It is given that a man invested $2, 000

The Principal is $2, 000

rate is 6% = 0.06

When t = 19

`FV=2000(1+0.06)^(19)=2000(1.06)^(19)\approx\$6051`

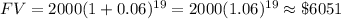
In 19 years there will be $6051

For the man to have a future value double of the man's investment;

`\begin{gathered} 4000=2000(1.06)^t \\ \\ \Rightarrow2=(1.06)^t \\ \\ \text{ taking }ln\text{ of bothn sides} \\ \\ \Rightarrow\ln2=t\ln(1.06) \\ \\ \Rightarrow t=(\ln2)/(\ln(1.06))\approx12 \end{gathered}`

Therefore, it will take up to 12 years for the man's investment to double.