To answer this question, we need to know that we are dealing here with the standard normal distribution. In this distribution, we have z-scores. These z-scores are values for which we can find the probabilities of any normally distributed data if we find the corresponding z-score using the next formula:

Where
• x is the raw value
,
• μ is the mean for the population
,
• σ is the standard deviation for the population
Finding the area under the standard normal curve to the right of z = 1.03
In the standard normal distribution, we have that the mean for the population is zero, μ = 0, and the standard deviation is equal to 1, σ = 1. Then, we can say that the standard normal distribution is a special case for the normal distribution.
When we have a value for z = 1.03, we have a "normalized" value, and we can find the area under the standard normal distribution for this value of z. We will find the cumulative probability until this number, z = 1.03. Then, we have the next graph to show this:
This is the area under the standard normal distribution and this area is given by tables in any Statistics books, or on the internet, and graphing calculators too.
This area is, according to the graphing calculator used, equal to:
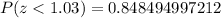
To consult a standard normal distribution, we need to identify the value for z at the right column of the table. Many tables have at the top one arrow in which we have more decimals of the z-score as 0.01, 0.02, 0.03, and so on, so we have values at the left column like 1. If we need to find a value of 1.03, we need to use 1 and the value at the top (0.03). The point at which these two values intersects is the value for the cumulative probability of the standard normal distribution (the area at the left of the given value). We need to take care that the given values are for the cumulative values of the function.
Using a table from the internet, we have that the value for the area under z =1.03 is 0.84849.
However, this is the area to the left of z = 1.03. To find the area to the right of z = 1.03, we need to subtract the corresponding probability from 1 as follows:
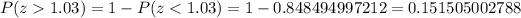
We can see this graphically as follows:
And this area is equivalent to 0.1515 (rounding to four decimal places). We can see that the area is to the right of z = 1.03.
Finding the area under the standard normal curve between z = 0.17 and z = 2.06
To find this area, we need to find the cumulative probability (the area at the left) of z = 0.17 and the area at the left (cumulative probability) of z = 2.06. Then, we need to subtract the area at the left of z = 0.17 from the area given by z = 2.06 (also at the left of z = 2.06).
Then, the corresponding areas are (using a graphing calculator):
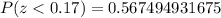
If we use a table from the internet, we have:
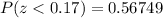
And we can visualize this area as follows:
As we can see the mean of the standard normal distribution is μ = 0, and z = 0.17 is slightly at the right of the population mean. The mean for the population is represented by z = 0.
The probability for the area under the curve for z = 2.06 is:
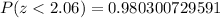
Using a standard normal table from the internet, we have:

And we can visualize it as follows:
Therefore, to have the area between z = 0.17 and z = 2.06, we need to subtract the cumulative area of z = 0.17 from z = 2.06. Then, we have:
[tex]P(0.17Then, we have:[tex]P(0.17Or we can say (rounding to four decimal places):[tex]P(0.17We can visualize it as follows:
In summary, we have:
• The area under the standard normal curve to the right of z = 1.03 is ,0.151505002788,. If we round the result to four decimal places, we have ,0.1515,. For five decimal places ---> ,0.15151,.
,
• The area under the standard normal curve between z = 0.17 and z = 2.06 is ,0.412805797916,. If we round the result to four decimal places, we have ,0.4128,. For five decimal places ---> ,0.41281,.