Question

Angie divides the polynomial function by (x+3). What can she conclude from the fact that the remainder is equal to 0

Answer 1

Step 1

Given;

`\begin{gathered} f(x)=x^3+3x^2-7x-21\text{ divided by (x+3)} \\ \end{gathered}`

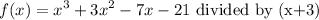
Step 2

use synthetic division to simplify the problem

`\begin{gathered} \text{coefficient of the }numerator \\ \end{gathered}`

1 3 -7 -21

`Write\text{ the problem in synthetic division format}`

Hence the function can be rewritten as

`((x+3)(x^2-7))/((x+3))`

Therefore the answer after will be;

`x^2-7`

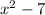
Since the remainder is 0, Angie can conclude that the dividend is divided evenly by the divisor and that the divisor is a factor of the dividend.