Given:
The interval is,
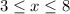
To find:
The average rate of change of the function
Step-by-step explanation:
Fromthe graph,
When x = 3,
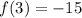
When x = 8,
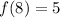
The graph is,
The formula for the average rate of the function is,
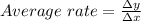
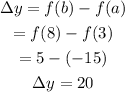

On substitution we get,
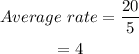
Final answer:
The average rate of change of the function is 4.