1 Answer

Aatwork · Answer 1 · 2023-06-24T20:52:52+0000

ANSWER

$0.314\operatorname{cm}$

Step-by-step explanation

The area of a sector is given as:

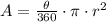
$A=(\theta)/(360)\cdot\pi\cdot r^2$

where r = radius of the circle

θ = angle of the sector

From the question, we do not have the radius, but we have the diameter of the circle.

The diameter of a circle is twice its radius, which means that:

$\begin{gathered} D=2\cdot r \\ r=(D)/(2) \\ r=(2)/(2) \\ r=1\operatorname{cm} \end{gathered}$

Therefore, the area of the sector is:

$\begin{gathered} A=(36)/(360)\cdot\pi\cdot1^2 \\ A=0.314\operatorname{cm}^2 \end{gathered}$

Please log in or register to add a comment.