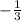Question

Does the limit exists? What’s the value if it does exist?Calculus early transcendental functions

Answer 1

`\text{The value is -}(1)/(3)`

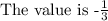
Given

`\lim _(x\to\infty)(2x^2(x-3))/(3x^2(1-2x))`

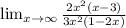
Solution

Let take the common factor first

`(2)/(3)\lim _(x\to\infty)(x^2(x-3))/(x^2(1-2x))`

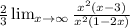
Let's apply algebraic property:

`a+b=a(1+(b)/(a))`
`\begin{gathered} (2)/(3).\lim _(x\to\infty)(x^2(x-3))/(x^2(1-2x)) \\ \\ (2)/(3).\lim _(x\to\infty)(x^2x(1-(3)/(x)))/(x^2x((1)/(x)-2)) \\ \\ x^2x\text{ can divide each other } \\ \\ (2)/(3).\lim _(x\to\infty)((1-(3)/(x)))/(((1)/(x)-2)) \end{gathered}`

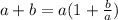
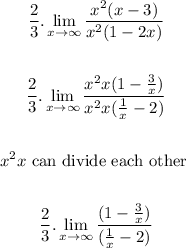
Let take the limit of the numerator

`\begin{gathered} \lim _(x\to\infty)(1-(3)/(x))=1 \\ \end{gathered}`

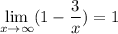
Also take the limit of the denominator

`\lim _(x\to\infty)((1)/(x)-2)=-2`

`we\text{ now have }(1)/(-2)`

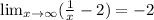
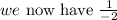
Now, let not forget the common factor outside

`(2)/(3).(1)/(-2)=(2)/(-6)=-(1)/(3)`

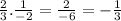
So therefore, the Limit exist and the value is

`-(1)/(3)`