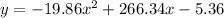Question

A rocket is shot off from a launcher. The accompanying table represents the height of the rocket at given times, where x is time, in seconds, and y is height, in feet. Write a quadratic regression equation for this set of data, rounding all coefficients to the nearest hundredth. Time in Seconds (x) Height in Feet (y) 0.8 195 1.9 429 2.7 569 3.8. 749 4.6 839 5.1 898 Fdit View Insert Format Tools Table

Answer 1

The form of the quadratic equation is

`y=ax^2+bx+c`

To find a, b, and c, we will any three points from the table and substitute x and y by them to make 3 equations and solve them

`\because x=0.8,y=195`

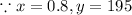
Substitute x by 0.8 and y by 195

`\begin{gathered} 195=a(0.8)^2+b(0.8)+c \\ 195=0.64a+0.8b+c \\ 0.64a+0.8b+c=195\Rightarrow(1) \end{gathered}`
`\because x=1.9,y=429`
`\begin{gathered} 429=a(1.9)^2+b(1.9)+c \\ 429=3.61a+1.9b+c \\ 3.61a+1.9b+c=429\Rightarrow(2) \end{gathered}`
`\because x=2.7,y=569`
`\begin{gathered} 569=a(2.7)^2+b(2.7)+c \\ 569=7.29a+2.7b+c \\ 7.29a+2.7b+c=569\Rightarrow(3) \end{gathered}`

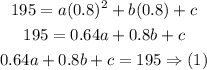
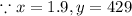
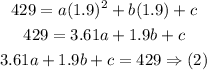
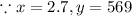
Now, we will use the calculator to solve this system of equations to find a, b, and c

a = -19.86

b = 266.34

c = -5.36

Substitute them in the form of the equation above

`y=-19.86x^2+266.34x-5.36`