Let's call X the length of the rectangular piece and Y the width of the rectangular piece.
First, the length of a rectangular piece of land is 90 yards more than three times its width. It means that we can write the following equation:
X = 90 + 3Y
Additionally, the perimeter is 780 yards, so we can write the equation:
2X + 2Y = 780
Therefore, replacing the first equation on the second equation and solving for Y, we get:

Now, we know that the width is equal to 75 yards, so we can calculated X as:
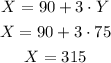
So, the length is 315 yards.
Answer: Length = 315 yards
Width = 75 yards