Question

Hello, I need help with this precalculus homework question, please?HW Q5

Answer 1

Given: The function below

`g(x)=-1+4^(x+2)`

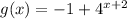
To Determine: The domain, range and the horizontal asymptote of the given function

Solution:

Step 1: Graph the function given

Step 2: Determine the domain

The domain is the set of input of a function where the function is real and defined.

From the graph above, it can be observed that the graph does not have an undefined point. Hence the domain is

`domain:(-\infty,\infty)`

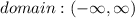
Step 3: Determine the range

The range of the function is the value of the output that is g(x) is the values of g(x) for which the function is real and defined

From the graph it can be observed that the function is defined at the point shown below

Hence, the range is

`\begin{gathered} Range:g(x)>-1 \\ Range:Interval\text{ Notation} \\ (-1,\infty) \end{gathered}`

Step 4: Determine the horizontal asymptote

A horizontal asymptote for a function is a horizontal line that the graph of the function approaches as x approaches ∞ (infinity) or -∞ (minus infinity). In other words, if y = k is a horizontal asymptote for the function y = f(x), then the values (y-coordinates) of f(x) get closer and closer to k as you trace the curve to the right (x→ ∞) or to the left (x → -∞).

From the graph, it can be observed that as we trace the graph to the left, y = -1. Hence, the horizontal asymptote is

`\begin{gathered} Horizontal\text{ asymptote} \\ g(x)=-1 \end{gathered}`

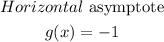
ANSWER SUMMARY

Domain: (-∞, ∞)

Range: (-1, ∞)

Horizontal Asymptote: g(x) = -1