Answer: (-∞,0)∪(0,∞)
Given:
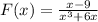
First, we need to find the restrictions for this given function. That would be: the denominator shall not be equal to 0.
With that, we will equate the denominator to 0 to find the value of x in which the function is undefined.
![\begin{gathered} x^3+6x=0 \\ x(x^2+6)=0 \\ x=0 \\ -------- \\ x^2+6=0 \\ x^2=-6 \\ x=\pm\sqrt[]{-6} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/a8wpu1ejuvl791cfe1h2s4g6g6im81wbuk.png)
With this, we now know that the x value should be equal to 0. Since ±√-6 is an imaginary number, we can ignore this result.
Therefore, the domain for the given function is (-∞,0)∪(0,∞).