Question

camilla leans a 18foot ladder against a wall so that it forms an angle of 71 with the ground. how high up the wall does the ladder reach? Round your answer to the nearest tenth of a foot if necessary

Answer 1

The wall is 17.0 ft from the point ladder touches the wall

Step-by-step explanation:

The length of the ladder = 18 ft

The angle the ladder makes with the wall = 71°

We need to find the distance betwen the base of the wall and the point the ladder touches the wall.

To solve this, we will do an illustration of the scenario:

Let x = distance between the base of the wall and the point the ladder touches the wall

To get x, we will apply sine ratio (SOH):

`\begin{gathered} si\text{ n }71\degree\text{ = }(opposite)/(hypotenuse) \\ \text{opposite = x, hypotenuse = }18 \\ \\ \sin \text{ }71\degree=\text{ }(x)/(18) \end{gathered}`
`\begin{gathered} x\text{ = 18(}\sin 71\degree) \\ x\text{ = 18(}0.9455) \\ x\text{ = 17.019} \\ To\text{ the nearest tenth, x = 17.0} \end{gathered}`

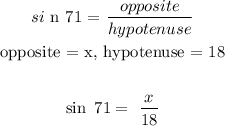
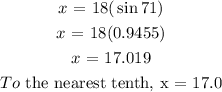
The wall is 17.0 ft from the point ladder touches the wall