1 Answer

Randomsolutions · Answer 1 · 2023-10-09T19:43:08+0000

In order to have similar triangles

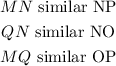
$\begin{gathered} MN\text{ similar NP} \\ QN\text{ similar NO} \\ MQ\text{ similar OP} \end{gathered}$

As we can see we have the measure of the 3 sides therefore the statement of similarity that we will use is SSS and the triangles that are similar are MNQ and PNO

The correct answer is d.

ANSWER

d. SSS triangle MNQ similar to triangle PNO

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

0 Comments

Please log in or register to add a comment.

Other Questions