Question

A golf ball slides down a pipe from the upper level of a miniature golf course and heads directly for the hole on the green. Unfortunately, another player’s ball is directly in the way. The second ball, which is initially at rest, moves forward with a speed of 4.0 m/s, causing it to land in the cup. The first ball comes to a complete stop after the collision. Both balls have a mass of 55 g. What is the first ball’s speed before the collision.

Answer 1

In a collision the total momentum is conserved, this means that:

`p_i=p_f`

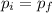
The momentum of each ball is given by:

`p=mv`

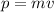
Then in this case we have:

`m_1v_1+m_2v_2=m_1v^(\prime)_1_{}+m_2v^(\prime)_2_{}`

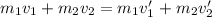
where one denotes the first ball and two denotes the second ball. We know that the second ball is initially at rest and that the first ball stops after the collision; we also know that the mass of each ball is 55 g, then we have:

`\begin{gathered} 0.055v_1+(0.055)(0)=(0.055)(0)+(0.055)(4) \\ 0.055v_1=0.22 \\ v_1=(0.22)/(0.055) \\ v_1=4 \end{gathered}`

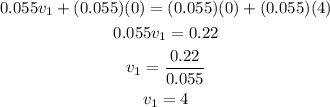
Therefore the speed of the first ball before the collision is 4 m/s