The given system of inequalities is:
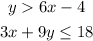
We can observe on the first inequality, it is in the slope-intercept form y>mx+b, where m is the slope and b is the y-intercept. So m=6 and b=-4.
Then, this inequality represents the line that intercepts the y-axis at -4.
Also, as this has the symbol ">", it means the line itself is not included in the solution, then it is a dotted line and its graph is:
Now, for the second inequality, we need to convert it to slope-intercept form:
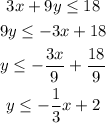
Then, it is represented by the line that intercepts the y-axis at y=2. As this inequality has the symbol "<=" then, the line is included in the solution set, it is a solid line, and the solution are the y-values lower or equal to the line, then it is represented by:
The solution set to the system, is the space where the solutions of both inequalities overlaps, and it is represented by the purple zone:
The answer is option D.